陶哲轩亲测：我用Gemini十分钟搞定了困扰学界多年的难题

陶哲轩携手Gemini，十分钟破解数学难题！

还是他本人擅长的连续整数结构的乘法数论问题。

该问题建立在前人并不完整的反证基础上，陶哲轩借助Gemini Deep Think进行证明补全。

全程只用了十分钟，Gemini就从论证分析打通了结论确认。

而这也并非孤例，陶哲轩发现，在Erdős问题网站上，类似的情况时有发生，最近陆陆续续有6个困扰数学界多年的Erdős难题通过AI辅助方法，得以解决。

还有许多研究者正在系统性地使用AI工具进行相关文献资料的查询，并作为解题思路留在评论区。

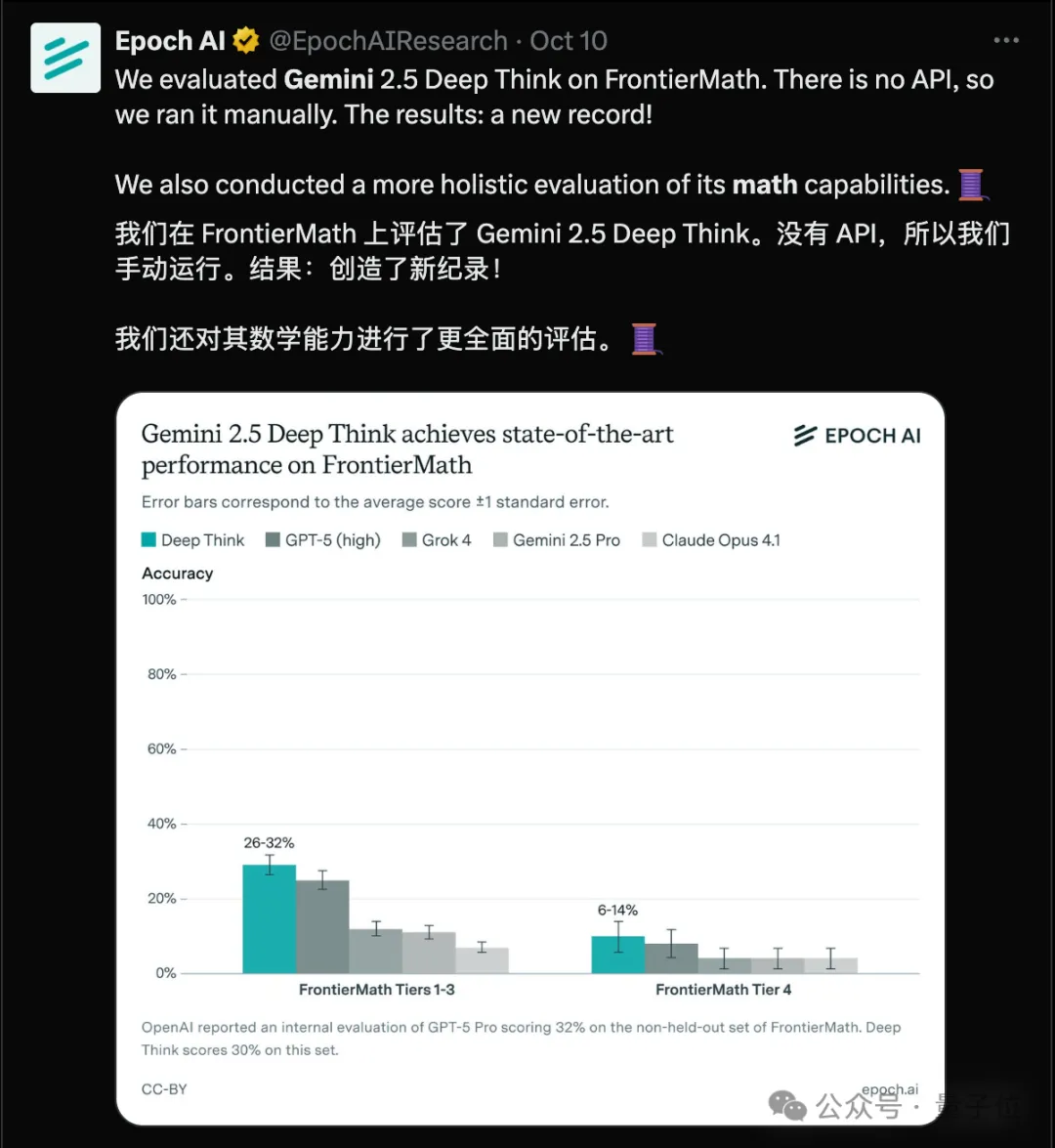
而这次陶哲轩使用的模型Gemini 2.5 Deep Think，想必大家也并不陌生。

正是此前的IMO金牌得主，在最新的FrontierMath测试中，其数学能力也远超GPT-5(high)等模型。

下面来看详细验证过程：

Gemini用十分钟完成验证

首先回到问题本身，这是由Paul Erdős提出的#367号问题：

该问题设定为整数n的2-full部分，即，其中为中幂为1的素因子之积。

简单来说，就是会把中所有只出现一次的素因子去掉，只保留指数至少为2的部分。

然后对于任意固定的，是否存在常数，使得对所有足够大的均满足：

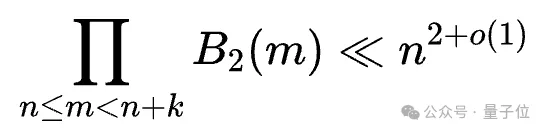
甚至再极端一些，满足。

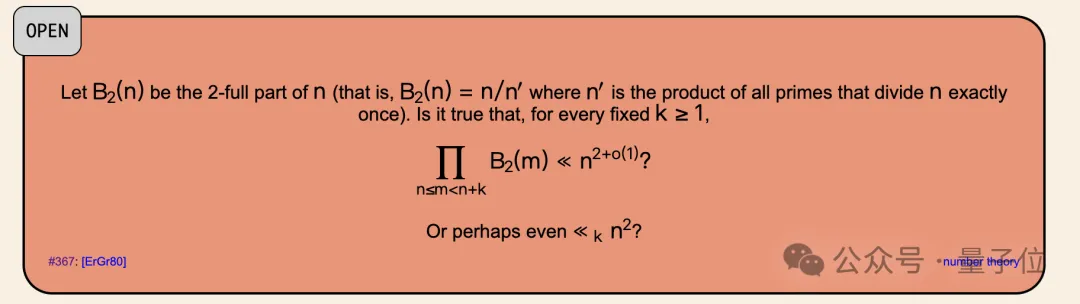
换言之，就是需要验证该条件中的极限上确界是否存在。

而就在几天前，数学家Wouter van Doorn对该问题的第二部分，基于一个未验证的同余恒等式，提出了相应的反证。

陶哲轩注意到了这个过程，于是将该恒等式连同问题本身一起交给了Gemini Deep Think进行完整证明，并确认整个论证过程。

结果只用了十分钟，Gemini就完成了上述过程。

在此基础上，陶哲轩又用了半小时，手动将Gemini的p-adic代数数论证明转换为更为基础的论证方式。

两天后，Boris Alexeev使用Harmonic的Aristotle工具（可直接从英语/LaTeX源代码中自动形式化处理），完成了对该证明的Lean形式化，总耗时两到三小时。

至此，该问题在Gemini和人类数学家的协同合作下，得以解决。

后续，陶哲轩为了完整起见，还额外用ChatGPT DeepResearch和Gemini DeepResearch进行了相关文献查询。

它们都能识别出该内容属于#367 问题，但在与之密切相关的问题#366 上仍然会存在混淆的情况出现。

二者均提及了与#367 和 #366 相关的佩尔方程构造，以及在连续幂数（特别是假设abc猜想成立的情况下）的最新进展，但它们都没有发现，在问题页面下方的评论处已经出现了对该问题第二部分的证伪，并且仍然宣称该问题尚未得到解决。

One More Thing

事实上，这已经不是陶哲轩第一次用AI辅助解决数学工作，早在三年前ChatGPT刚发布时，他就敏锐地察觉到AI将在数学证明上大有所为。

虽然最初的结果并不让他满意，但随着模型数学推理能力的进步，AI已经能够和数学家配合默契：

在AI的协助下，数学将在未来拥有更多的实验，而不仅仅是理论。

而对于那些对数学领域抱有热忱，但缺乏相关知识学习的人来说，AI也将帮助他们达到难以想象的深度。

不过也有网友表示，要警惕AI幻觉错误，AI的验证过程往往隐藏着容易被忽略的基础错误，这时候就需要数学家细心纠正。

这也是陶哲轩一直以来的观点，AI不会完全取代数学家，而是充当数学家证明的中介。

AI将帮助数学家发现其它可以探寻的路径。

参考链接：

[1]https://mathstodon.xyz/@tao/115591487350860999

[2]https://news.ycombinator.com/item?id=46017972

[3]https://www.erdosproblems.com/forum/thread/367

文章来自于“量子位”，作者“鹭羽”。