在人类的思维中,语言和视觉紧密交织,塑造着我们感知和理解世界的方式。我们的推理能力深深植根于语言思维和视觉记忆之中。那么,当我们将这些能力赋予人工智能时,会发生什么呢?如今的大语言模型已经展现出卓越的推理能力,但我们不禁思考:它们能否通过掌握视觉理解的力量,攀登认知能力的新高峰?
设想一下,一个人工智能能够像物理学大师一样,面对复杂的物理问题,沉着冷静地通过逻辑推理找到解决方案。正是这样的愿景激发我们创造了 QVQ —— 一个基于 Qwen2-VL-72B 构建的开源多模态推理模型(注:QVQ 的发音为 /kwik/)。
QVQ 在人工智能的视觉理解和复杂问题解决能力方面实现了重大突破。在 MMMU 评测中,QVQ 取得了 70.3 的优异成绩,并且在各项数学相关基准测试中相比 Qwen2-VL-72B-Instruct 都有显著提升。通过细致的逐步推理,QVQ 在视觉推理任务中展现出增强的能力,尤其在需要复杂分析思维的领域表现出色。
QVQ-72B-Preview 是由 Qwen 团队开发的实验性研究模型,专注于增强视觉推理能力。尽管它的表现超出了预期,但仍有几个限制需要注意:
1. 语言混合与切换:模型可能会意外地混合语言或在语言之间切换,从而影响响应的清晰度。
2. 递归推理:模型可能会陷入循环逻辑模式,产生冗长的响应而无法得出结论。
3. 安全和伦理考虑:模型需要增强安全措施,以确保可靠和安全的性能,用户在部署时应保持谨慎。
4. 性能和基准限制:尽管模型在视觉推理方面有所改善,但它无法完全替代 Qwen2-VL-72B 的能力。此外,在多步骤视觉推理过程中,模型可能会逐渐失去对图像内容的关注,导致幻觉。
我们在 4 个数据集上评估 QVQ-72B-Preview,包括:
* MMMU:一个大学级别的多学科多模态评测集,旨在考察模型视觉相关的综合理解和推理能力。
* MathVista:一个数学相关的视觉推理测试集,评估拼图测试图形的逻辑推理、函数图的代数推理和学术论文图形的科学推理等能力。
* MathVision:一个高质量多模态数学推理测试集,来自于真实的数学竞赛,相比于MathVista具有更多的问题多样性和学科广度。
* OlympiadBench:一个奥林匹克竞赛级别的双语多模态科学基准测试集,包含来自奥林匹克数学和物理竞赛的8,476个问题,包括中国高考。每个问题都附有专家级别的注释,详细说明了逐步推理的过程。
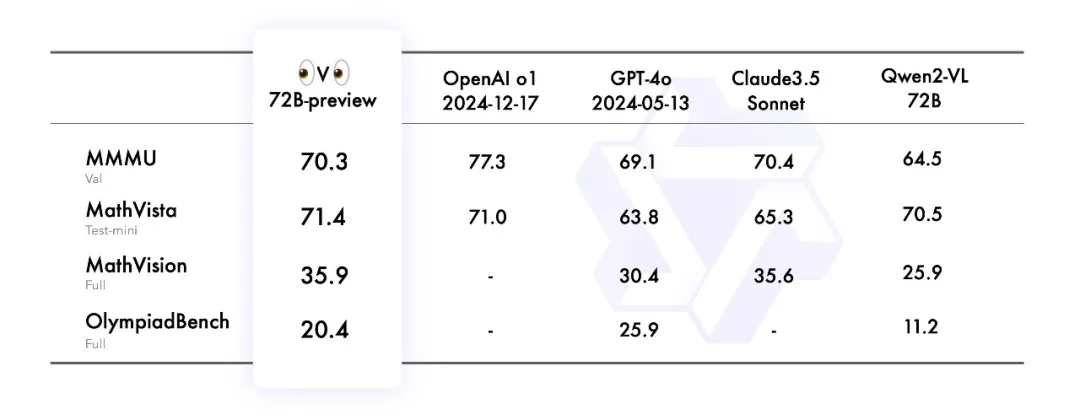
QVQ-72B-Preview 在 MMMU 基准测试中取得了 70.3 的分数,显著超越了 Qwen2-VL-72B-Instruct。此外,在剩下的三个专注于数学和科学问题的基准测试中,该模型表现出色,有效缩小了与领先的最先进的 o1 模型之间的差距。
以下,我们将展示几个示例,以说明该新模型在视觉推理任务中的应用。

Let’s tackle this problem step by step. So, we have two functions, f(x) and g(x), and their derivatives f’(x) and g’(x), tabulated for specific values of x. We’re asked to find h’(2), where h(x) is the product of f(x) and g(x). That means h(x) = f(x) * g(x).
First, I need to recall the product rule for derivatives. The product rule tells us how to find the derivative of the product of two functions. It states that if you have two differentiable functions u(x) and v(x), then the derivative of their product is given by:
(u*v)’(x) = u’(x)*v(x) + u(x)*v’(x)
So, in this case, u(x) is f(x) and v(x) is g(x). Therefore, h’(x) = f’(x)*g(x) + f(x)*g’(x).
Now, I need to find h’(2), which means I need to evaluate this derivative at x = 2.
Looking at the table:
Plugging these values into the product rule formula:
h’(2) = f’(2)*g(2) + f(2)*g’(2)
= (-8)(1) + (-3)(7)
= -8 + (-21)
= -29
Wait a minute, let me double-check that. Maybe I should consider if there’s any other way to approach this problem.
Another approach could be to consider the properties of derivatives and see if there’s a different way to compute h’(2). But I think the product rule is the most straightforward method here.
Let me verify the values from the table again:
These seem correct as per the table.
Alternatively, perhaps I should consider if the functions f(x) and g(x) have any special properties or if there’s a pattern I’m missing. For example, is g(x) a constant function? Looking at the table:
It doesn’t seem like g(x) is constant, as the values change. Similarly, f(x) is changing as well.
Maybe I should think about the units if this were a real-world problem, but since it’s an abstract mathematical problem, that might not help.
Alternatively, perhaps I should consider the geometric interpretation of the derivative. The derivative h’(2) represents the instantaneous rate of change of h(x) at x = 2. But again, that might not help in calculating the numerical value.
Let me try plugging in the values again to make sure I didn’t make a miscalculation.
h’(2) = f’(2)*g(2) + f(2)*g’(2)
= (-8)(1) + (-3)(7)
= -8 + (-21)
= -29
No, that seems correct.
Wait, maybe I should consider if the table has any units or if there’s a scaling factor I’m missing, but the problem doesn’t indicate any units, so I assume the values are just numerical.
Alternatively, perhaps there’s a typo in the problem or the table, but based on the given information, the calculation seems straightforward.
Let me consider if there’s a way to cross-verify this result. Suppose I were to consider the function h(x) = f(x)*g(x), and I want to find h’(2).
Another way to think about it is to consider the definition of the derivative:
h’(2) = lim[h -> 0] [h(2 + h) - h(2)] / h
But without knowing the explicit forms of f(x) and g(x), this approach isn’t practical because I can’t compute h(2 + h) for arbitrary h.
Therefore, relying on the product rule seems like the most appropriate method here.
So, my final answer is h’(2) = -29.
Final Answer
User:I want to know the volume of this sofa
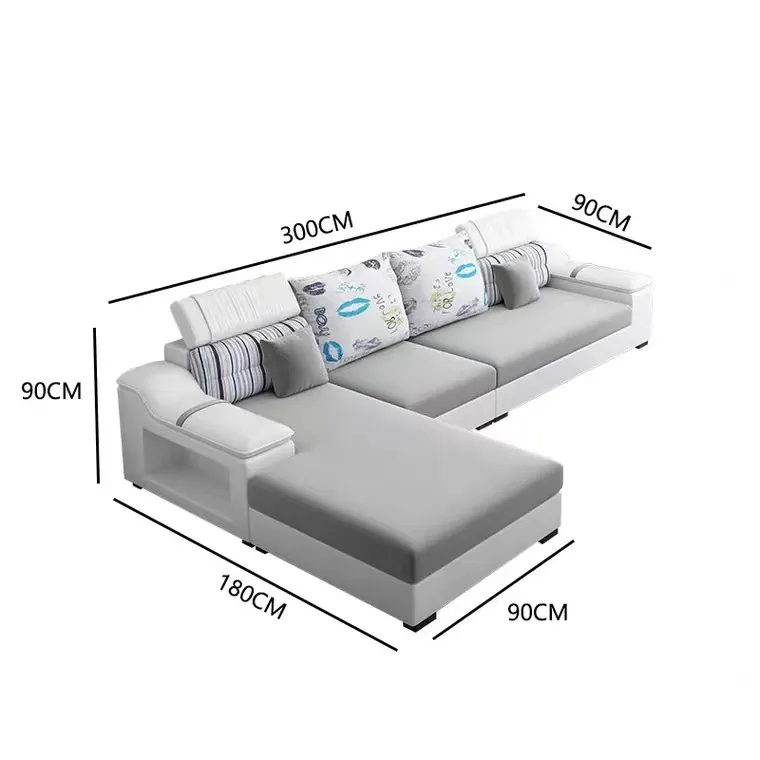
So I have this L-shaped sofa with dimensions provided, and I need to find its volume. The measurements are as follows:
First, I need to understand the shape and how it affects the volume calculation. An L-shaped sofa consists of two main parts: the straight section and the chaise lounge section.
Let me visualize this:
To find the volume, I should consider the sofa as a combination of rectangular prisms.
Perhaps I can divide the sofa into two parts:
Wait, but when I look at the dimensions, the chaise section is 180 cm in depth and 90 cm in width. However, since it’s an L-shape, the width of the chaise section might overlap with the straight section.
Let me double-check the dimensions.
Looking at the image:
I think the straight section is 300 cm in length and 90 cm in width, and the chaise section is 180 cm in depth and 90 cm in width, attached to the straight section.
In this case, the volume would be the sum of the volumes of these two sections.
First, calculate the volume of the straight section:
Volume_straight = length x width x height
Here, length = 300 cm, width = 90 cm, and height = 90 cm.
Volume_straight = 300 cm x 90 cm x 90 cm
Wait, but I need to confirm if the height is indeed 90 cm. The image shows a vertical dimension of 90 cm, which could be the height.
So, Volume_straight = 300 cm x 90 cm x 90 cm
Similarly, for the chaise section:
Volume_chaise = depth x width x height
Depth = 180 cm, width = 90 cm, height = 90 cm.
Volume_chaise = 180 cm x 90 cm x 90 cm
Then, the total volume would be Volume_total = Volume_straight + Volume_chaise
Let me calculate that.
First, Volume_straight = 300 cm x 90 cm x 90 cm = 2,430,000 cubic cm
Second, Volume_chaise = 180 cm x 90 cm x 90 cm = 1,458,000 cubic cm
Total volume = 2,430,000 + 1,458,000 = 3,888,000 cubic cm
But, I should consider if there’s any overlap or shared volume between the two sections.
Looking back, in an L-shape, the chaise section shares some space with the straight section, so perhaps simply adding the volumes isn’t accurate.
Maybe I should think of the entire sofa as a single rectangular prism with length 300 cm, width 180 cm (since the chaise adds 180 cm to the width), and height 90 cm.
Wait, but the width of the straight section is 90 cm, and the chaise adds another 90 cm to the width, making the total width 180 cm.
So, total dimensions would be:
Length: 300 cm
Width: 180 cm
Height: 90 cm
Therefore, total volume = length x width x height = 300 cm x 180 cm x 90 cm = 4,860,000 cubic cm
However, this seems larger than the previous calculation. Which one is correct?
Let me think again.
Option 1: Sum of two separate volumes:
Volume_straight + Volume_chaise = 2,430,000 + 1,458,000 = 3,888,000 cubic cm
Option 2: Entire sofa as one big rectangular prism:
Volume_total = 300 cm x 180 cm x 90 cm = 4,860,000 cubic cm
But this seems incorrect because it’s overcounting the shared space where the two sections meet.
So, Option 1 is more accurate.
Alternatively, perhaps I need to consider the chaise section as an extension that doesn’t add its full volume but only the additional volume it provides.
Wait, maybe I should subtract the overlapping volume.
Let me try another approach.
Consider the straight section as a rectangular prism: 300 cm x 90 cm x 90 cm.
The chaise section extends 180 cm in depth and 90 cm in width, but since it’s attached to the straight section, there is an overlap in width.
Actually, in an L-shape, the chaise section shares the width with the straight section, so the additional volume added by the chaise is only the part that doesn’t overlap.
Wait, this is getting complicated.
Maybe I should look at it differently.
Let’s consider the entire base area first.
The base of the sofa would be the area in contact with the floor.
The straight section is 300 cm in length and 90 cm in width.
The chaise section adds another 180 cm in depth, making the total width 90 cm + 180 cm = 270 cm.
Wait, no, if the straight section is 300 cm in length and 90 cm in width, and the chaise adds 180 cm in depth, then the base area would be a rectangle of 300 cm x 180 cm.
But that doesn’t account for the L-shape properly.
Alternatively, perhaps the base is L-shaped, with one side 300 cm and the other 180 cm, intersecting at a corner.
In that case, the total base area would be:
Area_base = (300 cm x 90 cm) + (180 cm x 90 cm) - (overlap area)
But what is the overlap area?
If the chaise section is attached to the straight section, the overlap would be the area where they connect.
Assuming they connect at a 90-degree angle, the overlap would be a square of side 90 cm.
Therefore, Area_overlap = 90 cm x 90 cm = 8,100 square cm
Thus, Area_base = (300 cm x 90 cm) + (180 cm x 90 cm) - 8,100 square cm
Calculate that:
(27,000 square cm) + (16,200 square cm) = 43,200 square cm
Minus 8,100 square cm = 35,100 square cm
Then, the height is 90 cm, so Volume_total = Area_base x height = 35,100 square cm x 90 cm = 3,159,000 cubic cm
This is different from both previous calculations.
Which one is correct?
I think this method accounts for the overlap properly.
Alternatively, perhaps I can use integration to find the volume, but that might be overkill for this problem.
Wait, another way: divide the sofa into smaller rectangular prisms whose volumes can be added up accurately.
Let’s try that.
Divide the sofa into three parts:
Then, Volume_total = (300 cm x 90 cm x 90 cm) + (180 cm x 90 cm x 90 cm) - (90 cm x 90 cm x 90 cm)
Calculate each part:
Volume_main = 300 cm x 90 cm x 90 cm = 2,430,000 cubic cm
Volume_chaise = 180 cm x 90 cm x 90 cm = 1,458,000 cubic cm
Volume_overlap = 90 cm x 90 cm x 90 cm = 729,000 cubic cm
Therefore, Volume_total = 2,430,000 + 1,458,000 - 729,000 = 3,159,000 cubic cm
This matches the previous calculation using the base area method.
So, the correct volume is 3,159,000 cubic cm.
But wait, earlier I thought the total base area was 35,100 square cm multiplied by 90 cm, which gives 3,159,000 cubic cm.
Yes, that seems consistent.
Therefore, the volume of the sofa is 3,159,000 cubic cm.
Final Answer
User:图片中的滤液E是什么化学物质?
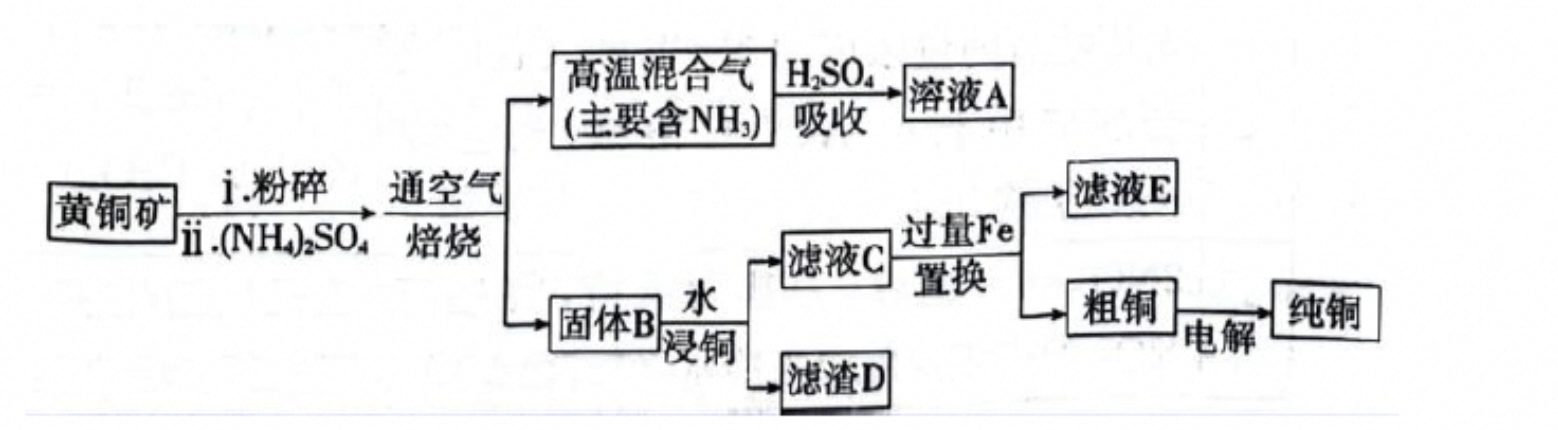
所以我在看这个流程图,是关于从黄铜矿中提取铜的。首先,黄铜矿被粉碎,然后和硫酸铵一起焙烧,通入空气。这个过程中会产生高温混合气,主要含有氨气,还有固体B。氨气用硫酸吸收得到溶液A,固体B用水浸铜,得到滤液C和滤渣D。滤液C加入过量铁粉进行置换,得到粗铜和滤液E。最后,粗铜通过电解得到纯铜。
我需要确定滤液E是什么化学物质。要弄清楚这个,我得先理解整个流程中发生了什么反应。
首先,黄铜矿主要成分是铜铁硫化物,化学式一般是CuFeS2。粉碎后和硫酸铵一起焙烧,通入空气,这个过程应该是在高温下发生氧化反应。
具体反应可能有:
4CuFeS2 + 9O2 + 2(NH4)2SO4 → 4CuSO4 + 2Fe2O3 + 2(NH4)2SO4 + 8SO2 + 4H2O
不过,这个可能不太对,因为生成物里有硫酸铜、氧化铁、硫酸铵、二氧化硫和水。但是,根据流程图,产生的高温混合气主要含氨气,所以可能我的反应写得不对。
或者,可能是这样的反应:
2CuFeS2 + 4O2 + (NH4)2SO4 → 2CuSO4 + 2FeO + (NH3) + SO2 + H2O
这样生成物里有氨气,符合流程图中的描述。
不过,我得再确认一下这个反应是否合理。
黄铜矿焙烧通常会产生二氧化硫,因为硫化物被氧化成二氧化硫。同时,硫酸铵可能分解产生氨气。
硫酸铵在高温下会分解:
(NH4)2SO4 → 2NH3 + H2SO4
产生的氨气和硫酸可以和黄铜矿的氧化产物反应。
所以,可能的反应是:
2CuFeS2 + 4O2 + 2NH3 + H2SO4 → 2CuSO4 + 2FeO + (NH4)2SO4 + 2H2O
这样,产生的高温混合气中主要含有氨气,因为硫酸铵分解产生的氨气。
然后,这个高温混合气用硫酸吸收,得到溶液A,应该是硫酸铵溶液:
NH3 + H2SO4 → (NH4)2SO4
接下来,固体B是焙烧后的残留物,包括CuSO4、FeO和可能的其他杂质。固体B用水浸铜,得到滤液C和滤渣D。
滤液C应该是含有铜离子的溶液,比如硫酸铜溶液。滤渣D可能是不溶于水的物质,比如铁的氧化物或其他杂质。
然后,滤液C中加入过量铁粉进行置换,得到粗铜和滤液E。
这个反应应该是:
Fe + CuSO4 → FeSO4 + Cu
所以,粗铜是被置换出来的铜,滤液E应该是硫酸亚铁溶液。
不过,我得确认一下,因为流程图中滤液E是单独存在的,可能还有其他成分。
或者,可能在加入铁粉时,铁不仅置换出了铜,还可能与其它金属离子反应。
但根据常见的湿法炼铜过程,通常是铁置换铜,得到硫酸亚铁和铜。
然后,粗铜通过电解精炼得到纯铜,这是常见的电解精炼过程。
所以,根据这个流程,滤液E应该是硫酸亚铁溶液。
不过,我得再检查一下,看看是否有其他可能性。
首先,黄铜矿焙烧产生的固体B,主要成分是CuSO4和FeO,可能还有其他杂质。
用水浸取后,得到滤液C,应该是硫酸铜溶液,滤渣D可能是不溶性的铁的氧化物等。
然后,滤液C中加入过量铁粉,发生反应:
Fe + CuSO4 → FeSO4 + Cu
这样,铜被置换出来,成为粗铜,滤液E是硫酸亚铁溶液。
这个逻辑是通的。
但是,我注意到流程图中滤液E是单独存在的,可能还有其他成分,或者有其他的用途。
或者,可能在加入铁粉时,铁还与其它金属离子反应,生成相应的盐类。
不过,根据常见的湿法炼铜工艺,主要是利用铁置换铜,得到硫酸亚铁和铜。
所以,滤液E应该是硫酸亚铁溶液。
为了确认这一点,我可以考虑一下硫酸亚铁的性质,以及在后续步骤中是否有用途。
硫酸亚铁可以作为电解液的组分,或者有其他的应用,但在这个流程图中没有显示。
或者,可能滤液E被回收利用,或者作为副产品出售。
不过,根据流程图,滤液E是单独存在的,没有进一步的处理,所以可能就是硫酸亚铁溶液。
所以,我的答案是滤液E是硫酸亚铁溶液。
答案
滤液E是硫酸亚铁溶液。
更多内容,详见Qwen团队技术博客:https://qwenlm.github.io/blog/
我们的愿景是开发一个「全能」和「智能」的模型,为了实现这一目标,我们正在增强我们的视觉语言基础模型,赋予其基于视觉信息的深度思考和推理的高级能力。在不久的将来,我们计划将更多的模态整合到一个统一的模型中,使其更加智能,能够应对复杂的挑战并参与科学探索。
目前,QVQ模型已在魔搭社区和HuggingFace等平台上开源,欢迎前往体验:
魔搭社区ModelScope模型链接:
https://modelscope.cn/models/Qwen/QVQ-72B-Preview
魔搭社区ModelScope体验链接:
https://modelscope.cn/studios/Qwen/QVQ-72B-preview
Huggingface:
https://huggingface.co/Qwen/QVQ-72B-Preview
推荐阅读:《大家都说通义大模型好,究竟好在哪?》
文章来自微信公众号 “ 通义千问 ”
