真·博士水平！GPT-5首次给出第四矩定理显式收敛率，数学教授只点拨了一下

GPT-5真不愧是博士水平的AI！

在数学教授引导下，它首次将定性的第四矩定理扩展为带有显式收敛率的定量形式。

简单来讲就是，原来的定理仅说明收敛会发生，却没有给出具体速度，而借助GPT-5，这项研究首次明确了收敛速率。

OpenAI联合创始人Greg Brockman对此表示甚是欣慰。

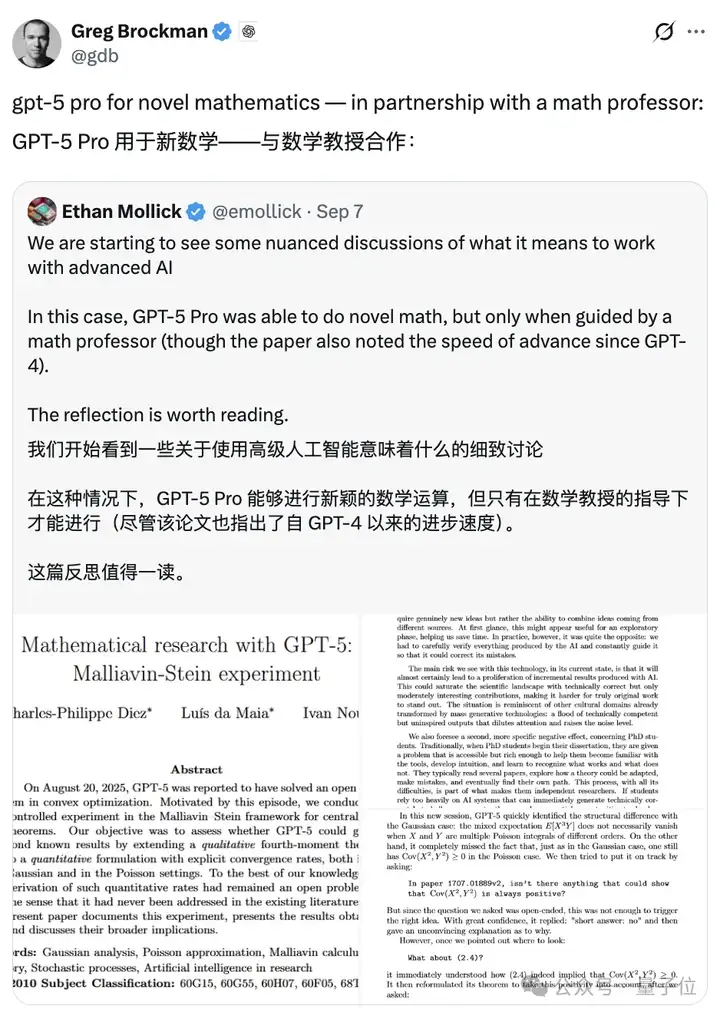
网友同样表示，真是奇迹。

借助GPT-5解决第四矩定理的定量收敛率

上个月，OpenAI研究人员Sebastien Bubeck称，GPT-5 Pro在数分钟内解决了凸优化领域的一个开放性问题，将已知的边界值从1/L改进为1.5/L。

受此启发，三位数学教授在Malliavin–Stein框架下开展了一项对照实验。

目标在于考察GPT-5能否突破既有成果，将定性的第四矩定理推广为带有显式收敛率的定量形式，并涵盖高斯情形与泊松情形。

首先，研究人员从以下初始提示开始：

论文2502.03596v1建立了一个定性的第四矩定理，适用于两个Wiener–Itô积分（阶数分别为p和q）的和，其中p和q的奇偶性不同。

基于Malliavin–Stein方法（具体可参见1203.4147v3），你能否推导出一个针对总变差距离的定量版本，其收敛速率仅依赖于该和的第四阶累积量？

(具体分析步骤已省略，感兴趣的读者可阅读原论文。)

第一次互动效果非常显著，GPT-5给出了总体正确的结论，并采用了恰当的工具和方法。

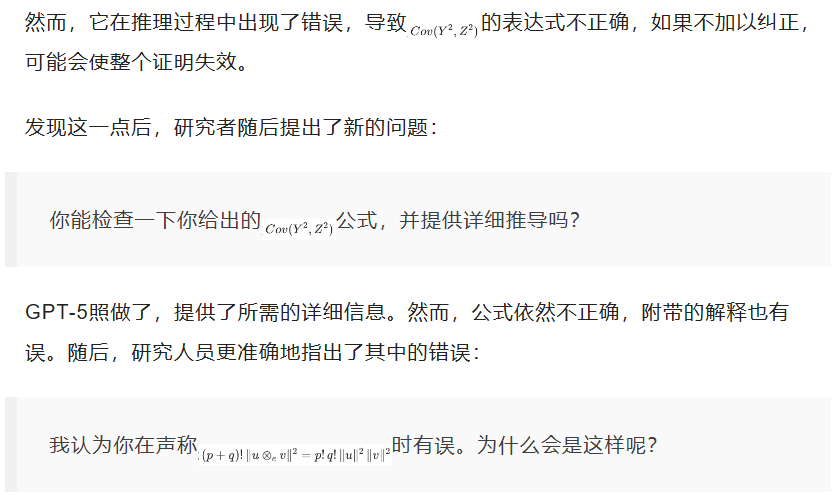
GPT-5最终承认该说法是错误的。但更重要的是，它理解了错误的来源。随后，继续给出了正确的推理过程和公式。

随后，应研究者的要求，GPT-5将最终结果整理成论文的格式，包括引言、主要定理的陈述、完整且正确的证明过程，以及参考文献。具体提示语如下：

请将此整理成一篇可投稿的研究论文，遵循我的风格（见附带论文0705.0570v4）：

• 以引言开始，提供一定的背景信息；
• 接着陈述主要结果，并给出非常详细的证明，确保每一步都完整；
• 最后附上完整的参考文献。

最终文档应为一个可编译的LaTeX文件。

最后，研究人员还让它增加一个结论部分，讨论该结果在未来研究中可能的拓展方向。

你能添加一个“结论与展望”部分吗？在其中总结主要内容，并提出未来研究可能的方向或拓展思路。

GPT-5依旧很听话，提出这个方法甚至可以推广到非高斯框架中。

扩展到泊松情形

基于这一建议，研究人员决定继续深入研究，尝试将其推广到泊松情形。

由于这时研究者发现上下文窗口已经相当长，可能会影响其性能，于是他们开启了一个新对话，并使用了如下提示：

这里有一篇论文（2502.03596v1），证明了两个奇偶性不同的Wiener–Itô积分之和的第四矩定理。我希望你能将其推广到泊松情形，使用论文1707.01889v2中包含的思路。

但是，由于研究者问的问题是开放性的，这还不足以触发正确的思路。GPT-5非常自信地回答道：“没有”，随后给出了一个不太令人信服的解释。

然而，一旦研究者指出具体信息:

那 (2.4) 呢？

GPT-5就能立刻将非负性考虑进去，并在研究者提出问题后，重新表述了定理。

One More Thing

有趣的是，作者最开始想将GPT-5列为共同作者提交论文，几个小时后，arXiv告诉他们，政策禁止将AI列为作者。

最后，他们只能提交作者列表中不含GPT-5的论文。

论文链接：https://arxiv.org/pdf/2509.03065v1

参考链接：

[1]https://x.com/gdb/status/1964474141295464675

[2]https://www.linkedin.com/posts/ivan-nourdin-61698a131_mathematical-research-with-gpt-5-activity-7368607852220805120-qLJA/?utm_source=share&utm_medium=member_desktop&rcm=ACoAAAzTDtoBh8KeVDRAqwRd0mUwfVpwfyirm80

[3]https://arxiv.org/abs/2502.03596

[4]https://arxiv.org/pdf/1707.01889

文章来自于“量子位”，作者“时令”。