ICLR 2026 | SEINT：高效的跨空间刚体不变度量

本文第一作者林俊一，共同第一作者薛敦耀来自中国人民大学。通讯作者为中国人民大学许洪腾副教授与孟澄助理教授。其他作者还包括来自北京理工大学的虞俊副教授。

在衡量 3D 点云、高分子构型等结构性数据之间的距离关系时，一个关键要求是对刚体/等距变换保持不变：即对样本施加旋转、平移后，分布间距离不应改变。本文将这一性质记为 SE(p) 不变性。

但要同时满足 SE(p) 不变性、严格的度量（Metric）性质，并具备高效且可扩展的计算，现有方法往往难以兼顾：要么需要显式求解几何对齐或引入复杂优化，计算开销高；要么计算更高效，却难以满足严格的度量性质，从而削弱其作为通用距离的理论保证与下游适用性。

为此，本文提出一种具有 SE(p) 不变传输性质的度量 SEINT：通过构造无需训练的 SE(p) 不变表示，将高维结构信息压缩为可用于 Optimal Transport (OT) 对齐的一维表征，从而在保持不变性与严格度量性质的同时显著提升效率。

• 代码地址：https://github.com/junyilin559/SEINT
• 论文地址：https://openreview.net/forum?id=oyxExc7TEl

要点速览

• 新表征：本文创新性地提出了两种等距不变的分布表征（PTD / DcPTD），无需训练即可将任意维度空间中的分布映射为一维表示。

• 新度量：基于上述一维表示构建由一维 OT 对齐实现的 SE(p) 不变距离 SEINT，该距离可被严格证明为在范数空间等距类上的度量。

• 跨空间：除旋转/平移不变外，SEINT 还能比较任意等距类分布，因此支持跨空间分布距离的定义。

• 可拓展：SEINT 方法目前已在范数空间得到了广泛应用，其形式还可进一步拓展到任意度量空间中。

最优传输（OT）在分布匹配与对齐任务中应用广泛，也是衡量分布差异的核心工具之一。但当我们希望一个距离同时满足：SE(p)（旋转 + 平移）不变、严格的度量性质（Metric）、以及可扩展的高效计算时，现有方法往往难以兼顾这些方面。通常来说，强调度量性与等距不变性的内蕴式（基于关系结构）方法计算代价较高；而更快的外蕴式/表征式对齐虽高效，却难同时保证这些理论性质。

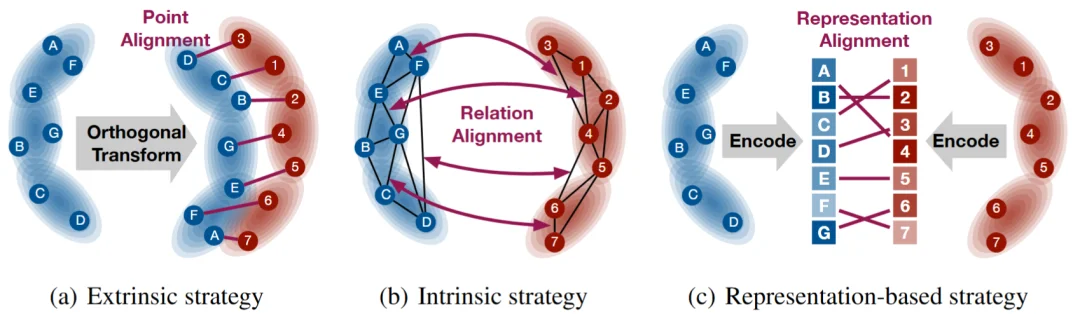
三类 SE(p) 不变的对齐策略：外蕴式、内蕴式与表征式

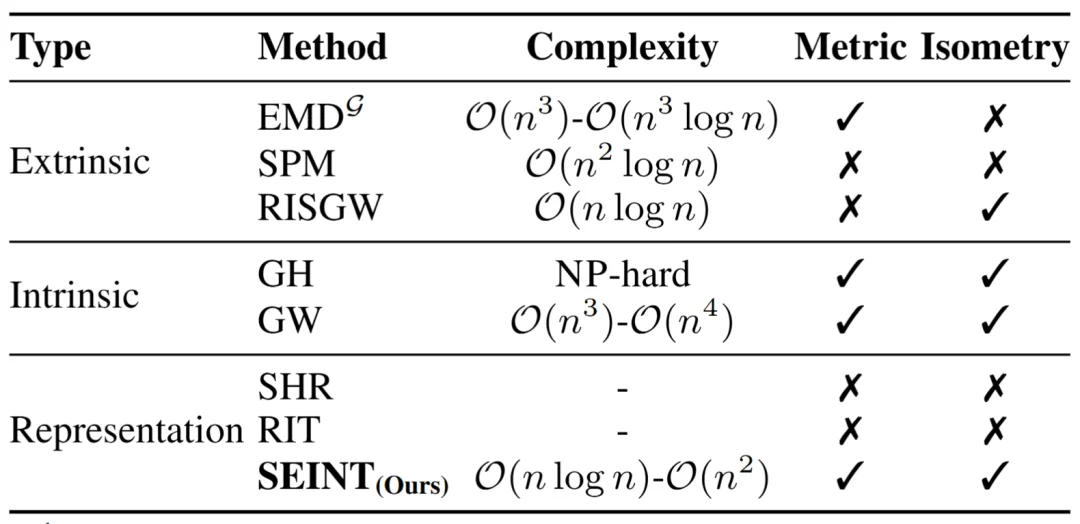
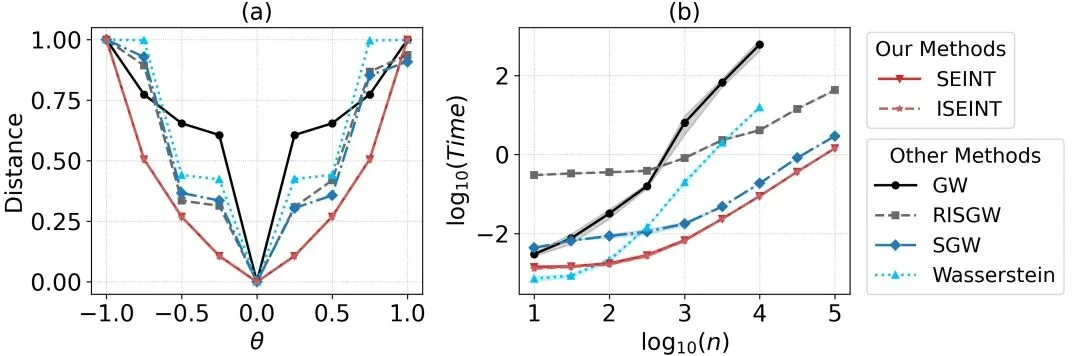
SEINT在计算/度量/跨空间指标上表现优异

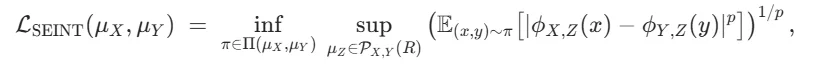
其中，inf 表示在两侧分布间寻找最优耦合（对齐方式），而 sup 则表示在候选参考分布中选择最能区分两者差异的「最不利」参考，以减弱参考选择的偶然性，并支撑其 Metric/Isometry 相关性质。SEINT 方法流程图如下。

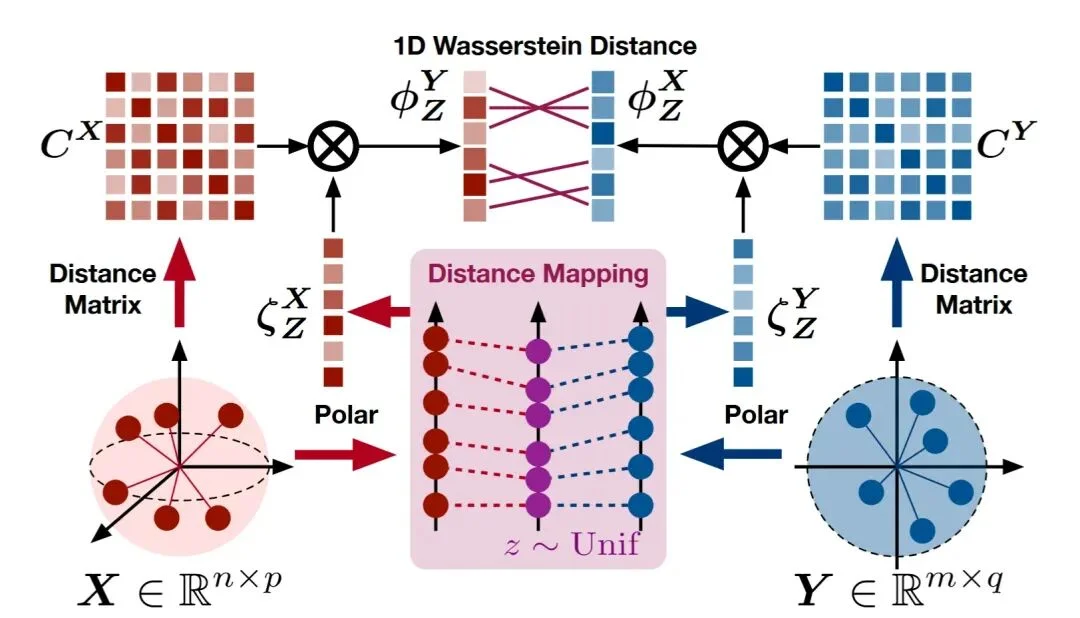
SEINT 的数值实现流程示意图。 给定来自两个空间的分布，先取样本范数；再结合随机一维参考 z 计算 PTD，并与距离矩阵卷积得到 DcPTD；最后计算两侧 DcPTD 的一维 Wasserstein 距离，得到 SEINT。

实验

本文从作为度量指标（Distance Metric）的几何性质和作为正则化项（Regularizer）的下游应用两个核心维度出发，与现有的多个 OT 基线方法进行了全面比较。

• 严格的 SE(p) 不变性与极高的计算效率

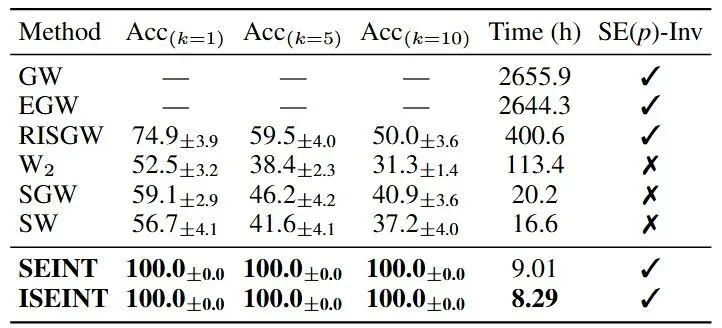
此外，本文通过多维缩放（MDS）展示了不同度量方法在旋转干扰下的表现。如下图所示，在对原始点云施加随机旋转后，只有 SEINT、GW 和 AE 能够完美保留数据原本的闭环几何拓扑结构，而 SW 和 SGW 的结构则完全崩塌。这一直观结果再次强有力地证明了 SEINT 在处理几何对称性方面的优越性，且其计算代价远低于 GW。

• 跨空间比较能力与高维稳定性

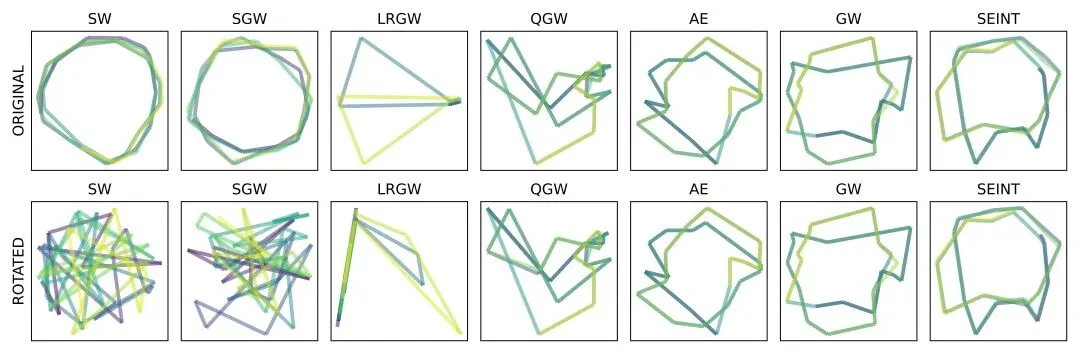
本文进一步评估了 SEINT 在跨空间（Cross-Space）场景下的表现。在 Horse-Gallop 实验中，SEINT 成功通过比较 2D 投影与 3D 参考空间，准确捕捉到了马匹奔跑的步态周期，展现了比 EGW 更强的几何结构感知力。

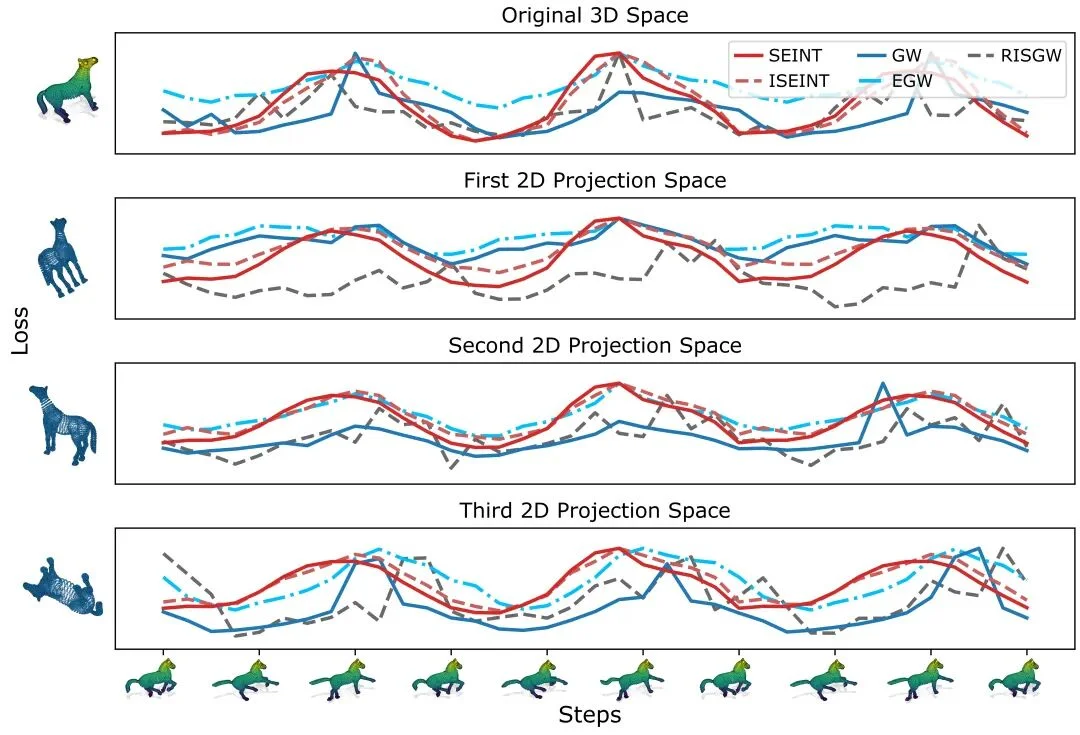
此外，在高维混合高斯数据的测试中，SEINT 克服了常见的「维度灾难」，随着分布差异的增大，其距离度量保持了平滑且单调的增长趋势，表现出优于其他 OT 方法的数值稳定性。

• 下游任务 SOTA：3D 分子生成

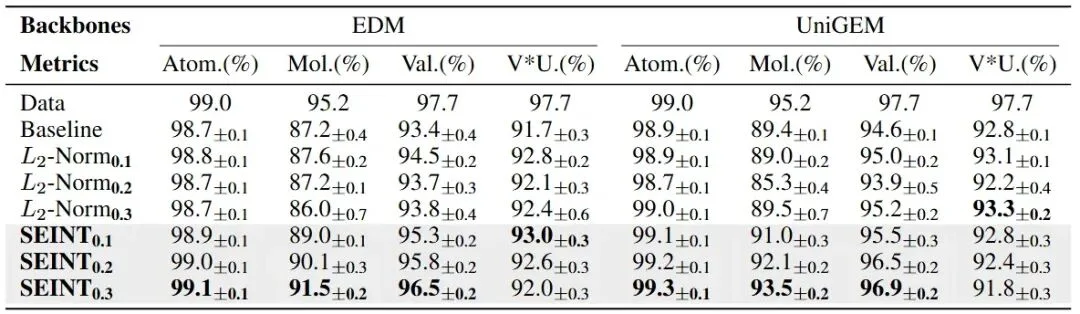
为了验证其实用价值，本文将 SEINT 作为正则化项集成到主流的扩散生成模型（EDM 和 UniGEM）中，在 QM9 和 GEOM-Drugs 数据集上进行了预训练和微调实验。下表结果显示，引入 SEINT 显著提升了生成分子的原子稳定性（Atom Stability）和分子稳定性（Mol Stability）。特别是在 UniGEM 模型中，SEINT 帮助模型在关键指标上达到了 State-of-the-Art (SOTA) 的性能，证明了其能够有效引导模型学习正确的几何结构。

总结

本文提出了一种新的表征路径：引入了两种无需训练的无监督表征技术（PTD 与 DcPTD），直接生成具有 SE(p) 不变性的 1D 特征，为构建不变性度量奠定基础。

本文奠定了坚实的度量基础：从理论上证明了 SEINT 是赋范空间等距类上的一个严格度量，该性质保证了数据嵌入的 SE(p) 不变性，并支持跨空间的分布比较。

文章来自于微信公众号 "机器之心"，作者 "机器之心"